Group-By Modeling in R Made Easy

There are several aspects of the R language that make it hard to learn, and repeating a model for groups in a data set used to be one of them. Here I briefly describe R’s built-in approach, show a much easier one, then refer you to a new approach described in the superb book,  R for Data Science, by Hadley Wickham and Garrett Grolemund.

For ease of comparison, I’ll use some of the same examples in that book. The gapminder data set contains a few measurements for countries around the world every five years from 1952 through 2007.

> library("gapminder")
> gapminder

# A tibble: 1,704 × 6
 country continent year lifeExp pop gdpPercap
 <fctr> <fctr> <int> <dbl> <int> <dbl>
1 Afghanistan Asia 1952 28.801 8425333 779.4453
2 Afghanistan Asia 1957 30.332 9240934 820.8530
3 Afghanistan Asia 1962 31.997 10267083 853.1007
4 Afghanistan Asia 1967 34.020 11537966 836.1971
5 Afghanistan Asia 1972 36.088 13079460 739.9811
6 Afghanistan Asia 1977 38.438 14880372 786.1134
7 Afghanistan Asia 1982 39.854 12881816 978.0114
8 Afghanistan Asia 1987 40.822 13867957 852.3959
9 Afghanistan Asia 1992 41.674 16317921 649.3414
10 Afghanistan Asia 1997 41.763 22227415 635.3414
# ... with 1,694 more rows

Let’s create a simple regression model to predict life expectancy from year. We’ll start by looking at just New Zealand.

> library("tidyverse")
> nz <- filter(gapminder, 
+              country == "New Zealand")
> nz_model <- lm(lifeExp ~ year, data = nz)
> summary(nz_model)

Call:
lm(formula = lifeExp ~ year, data = nz)

Residuals:
 Min 1Q Median 3Q Max 
-1.28745 -0.63700 0.06345 0.64442 0.91192

Coefficients:
 Estimate Std. Error t value Pr(>|t|) 
(Intercept) -307.69963 26.63039 -11.55 4.17e-07 ***
year 0.19282 0.01345 14.33 5.41e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8043 on 10 degrees of freedom
Multiple R-squared: 0.9536, Adjusted R-squared: 0.9489 
F-statistic: 205.4 on 1 and 10 DF, p-value: 5.407e-08

If we had just a few countries, and we wanted to simply read the output (rather than processing it further) we could write a simple function and apply it using R’s built-in by() function. Here’s what that might look like:

my_lm <- function(df) {
  summary(lm(lifeExp ~ year, data = df))
}
by(gapminder, gapminder$country, my_lm)
...
----------------------------------------------- 
gapminder$country: Zimbabwe

Call:
lm(formula = lifeExp ~ year, data = df)

Residuals:
 Min 1Q Median 3Q Max 
-10.581 -4.870 -0.882 5.567 10.386 

Coefficients:
 Estimate Std. Error t value Pr(>|t|)
(Intercept) 236.79819 238.55797 0.993 0.344
year -0.09302 0.12051 -0.772 0.458

Residual standard error: 7.205 on 10 degrees of freedom
Multiple R-squared: 0.05623, Adjusted R-squared: -0.03814 
F-statistic: 0.5958 on 1 and 10 DF, p-value: 0.458

Since we have so many countries, that wasn’t very helpful. Much of the output scrolled out of sight (I’m showing only the results for the last one, Zimbabwe). But in a simpler case, that might have done just what you needed. It’s a bit more complex than how SAS or SPSS would do it since it required the creation of a function, but it’s not too difficult.

In our case, it would be much more helpful to save the output to a file for further processing. That’s when things get messy. We could use the str() function to study the structure of the output, then write another function to extract the pieces we need, then apply that function, then continue to process the result until we get what we finally end up with a useful data frame of results. Altogether, that is a lot of work! To make matters worse, what you learned from all that is unlikely to generalize to a different function. The output’s structure, parameter names, and so on, are often unique to each of R’s modeling functions.

Luckily, David Robinson made a package called broom that simplifies all that. It has three ways to “clean up” a model, each diving more deeply into its details. Let’s see what it does with our model for New Zealand.

> library("broom")
> glance(nz_model)

  r.squared adj.r.squared sigma statistic p.value df
1 0.9535846 0.9489431 0.8043472 205.4459 5.407324e-08 2

   logLik      AIC    BIC   deviance df.residual
1 -13.32064 32.64128 34.096 6.469743     10

The glance() function gives us information about the entire model, and it puts it into a data frame with just one line of output. As we head towards doing a model for each country, you can imagine this will be a very convenient format.

To get a bit more detail, we can use broom’s tidy() function to clean up the parameter-level view.

> tidy(nz_model)
        term     estimate  std.error statistic p.value
1 (Intercept) -307.699628 26.63038965 -11.55445 4.166460e-07
2 year           0.192821  0.01345258  14.33339 5.407324e-08

Now we have a data frame with two rows, one for each model parameter, but getting this result was just as simple to do as the previous example.

The greatest level of model detail is provided by broom’s augment() function. This function adds observation-level detail to the original model data:

> augment(nz_model)

 lifeExp year  .fitted   .se.fit     .resid
1 69.390 1952 68.68692 0.4367774 0.70307692
2 70.260 1957 69.65103 0.3814859 0.60897203
3 71.240 1962 70.61513 0.3306617 0.62486713
4 71.520 1967 71.57924 0.2866904 -0.05923776
5 71.890 1972 72.54334 0.2531683 -0.65334266
6 72.220 1977 73.50745 0.2346180 -1.28744755
7 73.840 1982 74.47155 0.2346180 -0.63155245
8 74.320 1987 75.43566 0.2531683 -1.11565734
9 76.330 1992 76.39976 0.2866904 -0.06976224
10 77.550 1997 77.36387 0.3306617 0.18613287
11 79.110 2002 78.32797 0.3814859 0.78202797
12 80.204 2007 79.29208 0.4367774 0.91192308

        .hat    .sigma      .cooksd .std.resid
1 0.29487179 0.8006048 0.2265612817 1.04093898
2 0.22494172 0.8159022 0.1073195744 0.85997661
3 0.16899767 0.8164883 0.0738472863 0.85220295
4 0.12703963 0.8475929 0.0004520957 -0.07882389
5 0.09906760 0.8162209 0.0402635628 -0.85575882
6 0.08508159 0.7194198 0.1302005662 -1.67338100
7 0.08508159 0.8187927 0.0313308824 -0.82087061
8 0.09906760 0.7519001 0.1174064153 -1.46130610
9 0.12703963 0.8474910 0.0006270092 -0.09282813
10 0.16899767 0.8451201 0.0065524741 0.25385073
11 0.22494172 0.7944728 0.1769818895 1.10436232
12 0.29487179 0.7666941 0.3811504335 1.35014569

Using those functions was easy. Let’s now get them to work repeatedly for each country in the data set. The dplyr package, by Hadly Wickham and Romain Francois, provides an excellent set of tools for group-by processing. The dplyr package was loaded into memory as part of the tidyverse package used above. First we prepare the gapminder data set by using the group_by() function and telling it what variable(s) make up our groups:

> by_country <- 
+   group_by(gapminder, country)

Now any other function in the dplyr package will understand that the by_country data set contains groups, and it will process the groups separately when appropriate. However, we want to use the lm() function, and that does not understand what a grouped data frame is. Luckily, the dplyr package has a do() function that takes care of that problem, feeding any function only one group at a time. It uses the period “.” to represent each data frame in turn. The do() function wants the function it’s doing to return a data frame, but that’s exactly what broom’s functions do.

Let’s repeat the three broom functions, this time by country. We’ll start with glance().

> do(by_country, 
+    glance( 
+       lm(lifeExp ~ year, data = .)))

Source: local data frame [142 x 12]
Groups: country [142]

      country r.squared adj.r.squared sigma
    <fctr>      <dbl>      <dbl>    <dbl>
1 Afghanistan 0.9477123     0.9424835 1.2227880
2 Albania     0.9105778     0.9016355 1.9830615
3 Algeria     0.9851172     0.9836289 1.3230064
4 Angola      0.8878146     0.8765961 1.4070091
5 Argentina   0.9955681     0.9951249 0.2923072
6 Australia   0.9796477     0.9776125 0.6206086
7 Austria     0.9921340     0.9913474 0.4074094
8 Bahrain     0.9667398     0.9634138 1.6395865
9 Bangladesh  0.9893609     0.9882970 0.9766908
10 Belgium    0.9945406     0.9939946 0.2929025

# ... with 132 more rows, and 8 more variables:
# statistic <dbl>, p.value <dbl>, df <int>,
# logLik <dbl>, AIC <dbl>, BIC <dbl>,
# deviance <dbl>, df.residual <int>

Now rather than one row of output, we have a data frame with one row per country. Since it’s a data frame, we already know how to manage it. We could sort by R-squared, or correct the p-values for the number of models done using p.adjust(), and so on.

Next let’s look at the grouped parameter-level output that tidy() provides. This will be the same code as above, simply substituting tidy() where glance() had been.

> do(by_country, 
+    tidy( 
+      lm(lifeExp ~ year, data = .)))

Source: local data frame [284 x 6]
Groups: country [142]

country term estimate std.error
    <fctr>      <chr>        <dbl>     <dbl>
1 Afghanistan (Intercept) -507.5342716 40.484161954
2 Afghanistan year           0.2753287  0.020450934
3 Albania     (Intercept) -594.0725110 65.655359062
4 Albania     year           0.3346832  0.033166387
5 Algeria     (Intercept) -1067.8590396 43.802200843
6 Algeria     year            0.5692797  0.022127070
7 Angola      (Intercept)  -376.5047531 46.583370599
8 Angola      year            0.2093399 0.023532003
9 Argentina   (Intercept)  -389.6063445 9.677729641
10 Argentina  year            0.2317084 0.004888791

# ... with 274 more rows, and 2 more variables:
# statistic <dbl>, p.value <dbl>

Again, this is a simple data frame allowing us to do whatever we need without learning anything new. We can easily search for models that contain a specific parameter that is significant. In our organization, we search through salary models that contain many parameters to see if gender is an important predictor (hoping to find none, of course).

Finally, let’s augment the original model data by adding predicted values, residuals and so on. As you might expect, it’s the same code, this time with augment() replacing the tidy() function.

> do(by_country, 
+ augment( 
+ lm(lifeExp ~ year, data = .)))
Source: local data frame [1,704 x 10]
Groups: country [142]

   country   lifeExp year .fitted  .se.fit
    <fctr>     <dbl> <int> <dbl>    <dbl>
1 Afghanistan 28.801 1952 29.90729 0.6639995
2 Afghanistan 30.332 1957 31.28394 0.5799442
3 Afghanistan 31.997 1962 32.66058 0.5026799
4 Afghanistan 34.020 1967 34.03722 0.4358337
5 Afghanistan 36.088 1972 35.41387 0.3848726
6 Afghanistan 38.438 1977 36.79051 0.3566719
7 Afghanistan 39.854 1982 38.16716 0.3566719
8 Afghanistan 40.822 1987 39.54380 0.3848726
9 Afghanistan 41.674 1992 40.92044 0.4358337
10 Afghanistan 41.763 1997 42.29709 0.5026799

# ... with 1,694 more rows, and 5 more variables:
# .resid <dbl>, .hat <dbl>, .sigma <dbl>,
# .cooksd <dbl>, .std.resid <dbl>

If we were to pull out just the results for New Zealand, we would see that we got exactly the same answer in the group_by result as we did when we analyzed that country by itself.

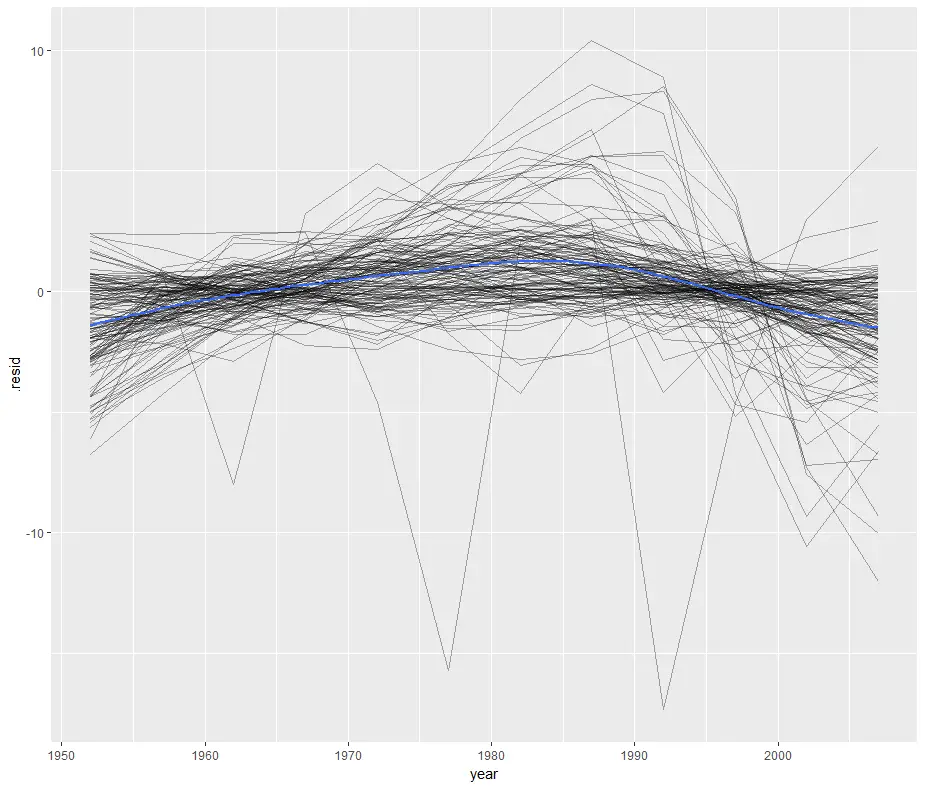
We can save that augmented data to a file to reproduce one of the residual plots from R for Data Science.

> gapminder_augmented <-
+ do(by_country, 
+   augment( 
+     lm(lifeExp ~ year, data = .)))
> ggplot(gapminder_augmented, aes(year, .resid)) +
+   geom_line(aes(group = country), alpha = 1 / 3) + 
+   geom_smooth(se = FALSE)

`geom_smooth()` using method = 'gam'

This plots the residuals of each country’s model by year by setting “group=country” then it follows it with a smoothed fit (geom_smooth) for all countries (blue line) by leaving out “group=country”. That’s a clever approach that I haven’t thought of before!

The broom package has done several very helpful things. As we have seen, it contains all the smarts needed to extract the important parts of models at three different levels of detail. It doesn’t just do this for linear regression though. R’s methods() function will show you what types of models broom’s functions are currently capable of handling:

> methods(tidy) 
 [1] tidy.aareg* 
 [2] tidy.acf* 
 [3] tidy.anova* 
 [4] tidy.aov* 
 [5] tidy.aovlist* 
 [6] tidy.Arima* 
 [7] tidy.betareg* 
 [8] tidy.biglm* 
 [9] tidy.binDesign* 
[10] tidy.binWidth* 
[11] tidy.boot* 
[12] tidy.brmsfit* 
[13] tidy.btergm* 
[14] tidy.cch* 
[15] tidy.character* 
[16] tidy.cld* 
[17] tidy.coeftest* 
[18] tidy.confint.glht* 
[19] tidy.coxph* 
[20] tidy.cv.glmnet* 
[21] tidy.data.frame* 
[22] tidy.default* 
[23] tidy.density* 
[24] tidy.dgCMatrix* 
[25] tidy.dgTMatrix* 
[26] tidy.dist* 
[27] tidy.ergm* 
[28] tidy.felm* 
[29] tidy.fitdistr* 
[30] tidy.ftable* 
[31] tidy.gam* 
[32] tidy.gamlss* 
[33] tidy.geeglm* 
[34] tidy.glht* 
[35] tidy.glmnet* 
[36] tidy.glmRob* 
[37] tidy.gmm* 
[38] tidy.htest* 
[39] tidy.kappa* 
[40] tidy.kde* 
[41] tidy.kmeans* 
[42] tidy.Line* 
[43] tidy.Lines* 
[44] tidy.list* 
[45] tidy.lm* 
[46] tidy.lme* 
[47] tidy.lmodel2* 
[48] tidy.lmRob* 
[49] tidy.logical* 
[50] tidy.lsmobj* 
[51] tidy.manova* 
[52] tidy.map* 
[53] tidy.matrix* 
[54] tidy.Mclust* 
[55] tidy.merMod* 
[56] tidy.mle2* 
[57] tidy.multinom* 
[58] tidy.nlrq* 
[59] tidy.nls* 
[60] tidy.NULL* 
[61] tidy.numeric* 
[62] tidy.orcutt* 
[63] tidy.pairwise.htest* 
[64] tidy.plm* 
[65] tidy.poLCA* 
[66] tidy.Polygon* 
[67] tidy.Polygons* 
[68] tidy.power.htest* 
[69] tidy.prcomp* 
[70] tidy.pyears* 
[71] tidy.rcorr* 
[72] tidy.ref.grid* 
[73] tidy.ridgelm* 
[74] tidy.rjags* 
[75] tidy.roc* 
[76] tidy.rowwise_df* 
[77] tidy.rq* 
[78] tidy.rqs* 
[79] tidy.sparseMatrix* 
[80] tidy.SpatialLinesDataFrame* 
[81] tidy.SpatialPolygons* 
[82] tidy.SpatialPolygonsDataFrame*
[83] tidy.spec* 
[84] tidy.stanfit* 
[85] tidy.stanreg* 
[86] tidy.summary.glht* 
[87] tidy.summary.lm* 
[88] tidy.summaryDefault* 
[89] tidy.survexp* 
[90] tidy.survfit* 
[91] tidy.survreg* 
[92] tidy.table* 
[93] tidy.tbl_df* 
[94] tidy.ts* 
[95] tidy.TukeyHSD* 
[96] tidy.zoo* 
see '?methods' for accessing help and source code
>

Each of those models contain similar information, but often stored in a completely different data structure and named slightly different things, even when they’re nearly identical. While that covers a lot of model types, R has hundreds more. David Robinson, the package’s developer, encourages people to request adding additional ones by opening an issue here.

I hope I’ve made a good case that doing group-by analyses in R can be done easily through the combination of dplyr’s do() function and broom’s three functions. That approach handles the great majority of group-by problems that I’ve seen in my 35-year career. However, if your needs are not met by this approach, then I encourage you to read Chapter 25 of R for Data Science (update: in the printed version of the book, it’s Chapter 20, Many Models with purrr and broom.) But as the chapter warns, it will “stretch your brain!”

If your organization is interested in a hands-on workshop that covers many similar topics, please drop me a line. Have fun with your data analyses!